Acompañando el Paseo de los Naranjos, sobre la calle interior principal del Campo Deportivo, además de las representaciones tridimensionales de cuerpos geométricos – donde los alumnos estudian matemáticas “en vivo” – se pueden apreciar dos murales que representan antiguos juegos infantiles: “El Trompo” y “El Aro” (con aros disponibles para usar); el Altar de los zapatitos rotos, la escultura de chatarra del Ingenioso Hidalgo Don Quijote de la Mancha, recreaciones a escala de los cuentos clásicos “Pinocho” y “Los tres cerditos” y una Cinta de Moëbius, que complementa las atracciones que brinda a los estudiantes el Paseo de la Geometría.

Paseo de la Geometría
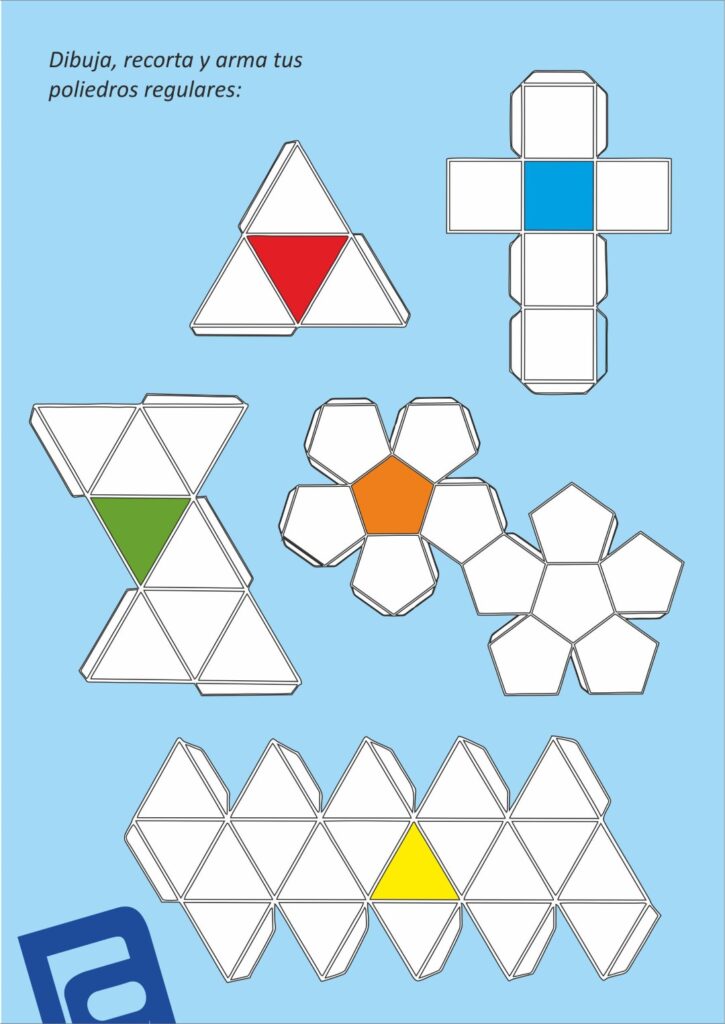
Sólo existen 5 poliedros regulares, también llamados “sólidos platónicos”:
TETRAEDRO REGULAR
Poliedro regular, de cuatro caras en forma de triángulos equiláteros, concurriendo tres a cada vértice.
HEXAEDRO REGULAR (CUBO)
Poliedro regular, de seis caras de forma cuadrada, concurriendo tres a cada vértice.
OCTAEDRO REGULAR
Poliedro regular, de ocho caras en forma de triángulos equiláteros, concurriendo cuatro de ellas a cada vértice.
DODECAEDRO REGULAR
Poliedro regular, de doce caras en forma de pentágonos regulares, concurriendo tres a cada vértice.
ICOSAEDRO REGULAR
Poliedro regular, de veinte caras en forma de triángulos equiláteros, concurriendo cinco a cada vértice.
PENTÁGONO REGULAR

Polígono convexo de cinco lados y cinco ángulos al vértice, iguales. Se inscribe en él, un polígono estrellado de cinco puntas también llamado “Estrella Pitagórica”.
Ambos se inscriben en una circunferencia, condición genérica a todos los polígonos regulares.
HEXÁGONO REGULAR

Sus lados son iguales al radio de la circunferencia circunscripta. Polígono estrellado de seis picos. Es la “Estrella de David” formada por dos triángulos equiláteros con sus respectivos vértices coincidiendo con los vértices del hexágono regular.
CIRCUNFERENCIA INSCRIPTA Y CIRCUNSCRIPTA A UN TRIÁNGULO

CIRCUNSCRIPTA
Es la que pasa por sus tres vértices. En todo triángulo existe una y sólo una circunferencia circunscripta a él. (Por tres puntos no alineados, existe siempre una circunferencia que pasa por los tres).
INSCRIPTA
Es tangente a los tres lados del triángulo. En todo triángulo existe una y sólo una circunferencia inscripta en él.
TEOREMA DE PITÁGORAS
En todo triángulo rectángulo, la suma de los cuadrados de los catetos, es igual, al cuadrado de la hipotenusa.